FUNGSI KUADRATIK (QUADRATIC FUNCTION) SIRI 1

Sekarang kita masuk kepada tajuk ketiga selepas Persamaan Kuadratik. Nama tajuk ketiga ini ialah FUNGSI KUADRATIK. Payah ke? Entah r. Bagi saya, mudah jew. Tetapi yang baru belajar Addmath, tentu nampak macam payah. He2

Quadratic function has the form ax2 + bx + c = 0 where a, b and c are numbers

You can sketch quadratic function in 4 steps. I will explain these steps in following examples.

Meh kita tngok cara nak menyelesaikannya. Anda jangan panik. Cool sahaja. Ikuti langkah-langkahnya sehingga selesai.

Example 1:

Sketch the graph of the quadratic function

f(x)=x2+2x−3

Solution:

In this case we have a=1,b=2 and c=−3

STEP 1: FIND THE VERTEC (BUCU)

To find x - coordinate of the vertex we use formula:

x=−b2a

Formula di atas sangat penting. Anda patut mendahului orang lain dengan mengetahui rumus di atas. Dalam Addmath, kita boleh guna apa sahaja cara yang kita ketahui.  

So, we substitute 1 in for a and 2 in for b to get

x=−b2a=−22⋅1=−1

JADI SEKARANG, KITA DAH DAPAT X = -1.

Kalau ada soalan tanya anda, apakah paksi simentri bagi graf di atas, jawapannya ialah x = -1.

To find y - coordinate, plug in x = -1  into the original equation
:

 y=f(−1)=(−1)2+2⋅(−1)−3=1−2−3=−4

Camne? Mudah ke? Bila anda dah dapat x = -1, maka seterusnya anda dapat cari nilai y. Masukan sahaja nilai x yang anda dapat ke dalam persamaan asal.

So, the vertex (bucu) of the parabola is (-1, -4). (−1,−4)

STEP 2: FIND THE Y- INTERCEPT.

Dalam membina graf, anda mesti tahu nilai pintasan-y. Caranya mudah sahaja, anggap x = 0. Masukkan nilai x = 0 ke dalam persamaan asal. 

Meh kita tengok penerangannya dalam BI.

To find y - intercept plug in x=0 into the original equation:

f(0)=(0)2+2⋅(0)−3=0−0−3=−3

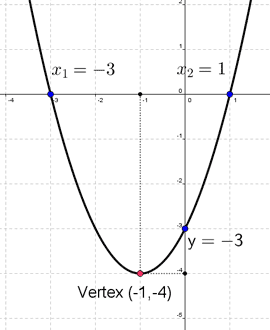
So, the y-intercept of the parabola is y=−3

STEP 3: FIND THE X-INTERCEPT. 

Sekarang kita cari pintasan x pulak. Mesti ada 2 nilai. Anggap sahaja y = 0. Meh kita tengok penerangannya dalam BI.

To find x - intercept solve quadratic equation f(x)=0 in our case we have
:

x2+2x−3=0

Solutions for this equation are:

x1=−3   and   x2=1

STEP 4: PLOT THE PARABOLA.

Sekarang mari kita lakarkan graf parabola yang anda dapat. Kalau nak tahu bagaimana nak membuatnya, meh kita tengok sekali lagi GRAF pada step 2. Graf itu dah cukup untuk membantu anda.



Example 2:

Sketch the graph of the quadratic function

f(x)=−x2+2x−2

Solution:

Dalam persamaan di atas, a adalah negatif sebab a= -1. Ia agak berbeza dengan persamaan sebelum ini.  Anda mesti tahu syarat-syarat sebelum ini. KALAU a > 1, dapat graf minimum. KALAU a < 1, dapat graf maximum. So graf dalam contoh (2) ini adalah MAXIMUM.

From the equation above,  we have a= -1, b = 2 and c =-2. So it is the maximum graf.

The x-coordinate of the vertex is:

x=−b2a=−22⋅(−1)=1

The y-coordinate of the vertex is
:

y=f(1)=−12+2⋅1−2=−1+2−2=−1

MAKA ANDA AKAN PEROLEHI VERTEC (BUCU) = (1, -1)



SENANG KAN. Bila anda dah dapat x = 1. Masukan sahaja nilai itu ke dalam persamaan asal, anda akan dapat y =1. Maka bucu (vertec) graf itu ialah (1, -1). He2. Senang, mudah & cepat.

Kalau ada soalan tanya anda, apakah paksi simentri graf itu (the axis of the symentry)?. Jawapan anda mesti jelas. x = 1


How to find the y-intercept?  Let x = 0.

y=f(0)=−02+2⋅0−2=−0+0−2=−2

How to find the x-intercept? Let y or f(x) = 0. In this case x-intercept doesn't exist. Bagaimana anda tahu? Meh saya tunjuk. Cari nilai b2 -  4ac. 

 Diberi a = -1, b = 2, c = -2. 

Maka (2)2 - 4 (-1)(-2) = 4 -  8 = -4.

Nilai -4 < 0. Maknanya punca-puncanya tak wujud (maya). Sebab itu ia tak menyentoh paksi x.

Try to use your calculator to get the value of x. You will get MATH ERROR. Thats means no root exist.


RUMAH. 28-1-2013.  5.36 PM
 f(x)=−x2+2x−2