CARA MEMAHAMI GRAF DALAM TRIGO (SIRI 1)

Terima kasih kepada semua peminat blog saya. Ucapan terima kasih itu kerana 2 sebab. [1] Sokongan anda yang berterusan kepada admin, [2] Kerana anda sudi membaca cerita-cerita sokongan saya.

Konsep saya terhadap pembinaan blog ini mudah sahaja. Sambil anda belajar Addmath, boleh juga anda membaca cerita selingan sebagai penguat jiwa, pembakar semangat, peningkat motivasi dan sebagainya.

Hari ini saya hendak focus kepada cara-cara membina graf dalam trigonometri.


PERHATIAN

Markah penuh hanya diberikan kepada graf dan perkara-perkara yang berkaitan sahaja. Tiada markah diberikan kepada rekabentok jadual kerja.

Mari kita mulakan dengan y = sin x

* We start with y = sin x.

* It has amplitude =1 and period =2π.

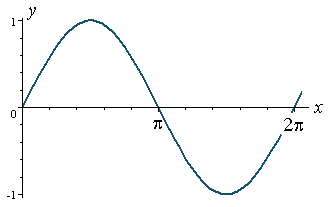
PERHATIAN

Ada 3 perkara yang sangat penting dengan graf di atas.

[1] Anda mesti ingat dengan betul cara nak melukis graf di atas.

[2] Boleh menukar nilai secara 2 hala

     π = 180 atau sebaliknya

    2π = 360 atau sebaliknya

[3] Tahu cara mencari nilai daripada graf

Jika y = 0, maka x = 0, π, 2π

Jika y = 1, maka x = 90

Jika y = -1, maka x = 270

Sekarang, kita tengok bentok graf y = 5 sin x

* Now let's look at the graph of y = 5 sin x.

* This time we have amplitude = 5 and period = 2π. (I have used a different scale on the y-axis.)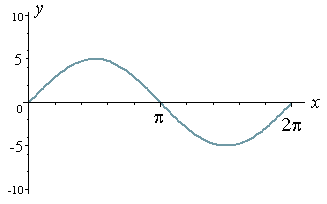

Maksudnya, kalau y = 5 sinx, anda darab sahaja 5 dengan semua nilai y yang anda dapat sebwlum ini. Nilai maksima akan jadi 5 X 1 = 5,  manakala nilai minimanya   pula akan jadi 5 X (-1) = -5. 

Sekarang mari kita tengok y = 10 sin x

* And now for y = 10 sin x.

* Amplitude = 10 and period = 2π.

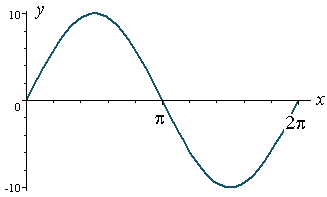
Hal yang sama akan berlaku sepertimana pada y = 5 sinx. Nilai maksima akan jadi 10, manakala nilai minima = -10.

PERHATIAN

Jika kita mengabungkan ketiga-tiga graf di atas , anda akan memperlehi pola berikut. 

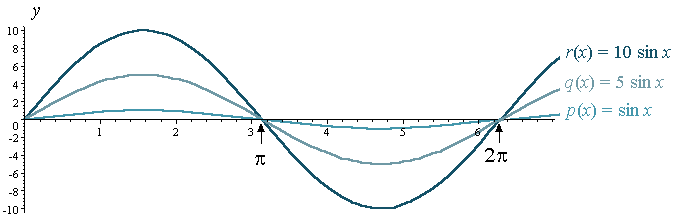
Sekarang, mari kita tengok y = kos x

* Now, lets we look to y = kos x.

PERHATIAN : Anda mesti ingat bentok graf ini sepertimana graf sebelum ini iaitu y = sin x. Daripada graf y = kos x ini, anda mendapat beberapa kseimpulan.

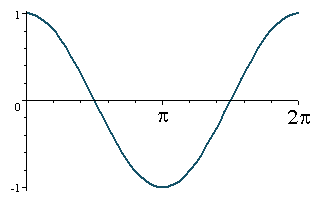
Ada 3 perkara juga yang sangat penting dengan graf di atas.

[1] Anda mesti ingat dengan betul cara nak melukis graf di atas.

[2] Boleh menukar nilai secara 2 hala

     π = 180 atau sebaliknya

    2π = 360 atau sebaliknya

[3] Tahu cara mencari nilai daripada graf

Jika y = 0, maka x =90, 270

Jika y = 1, maka x = 0, 360

Jika y = -1, maka x = 90

Hal yang sama berlaku jika anda menggunakan y = 5 kos x dan y = 10 kos x. Dan jika kita mengabungkan ketiga-tiga graf itu, hasilnya adalah seperyi berikut.

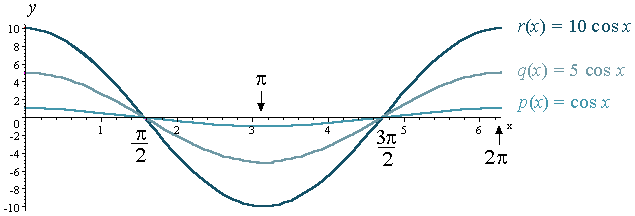
Sekarang mari kita tengok graph dari sebuah persamaan yang panjang.

Example 5: Graph y = 3cos(2x - π) + 1 

We start by noting what A, B, C and D are in the above equation.

 A = 3, B = 2, C = π and D = 1.

 So, that means that we are going to graph cos(x), but with some modifications.

The graph is stretched vertically by a factor of 3.

PERHATIAN : Rujuk kepada nilai A = 3. Graf ini akan ditarik menegak sebanyak 3 unit.   

The period is now 2π/2 = π instead of 2π.

PERHATIAN : Rujuk kepada nilai B = 2. Tempoh akan menjadi lebih singkat, menggunakan 2π / 2, di mana 2 itu adalah nilai B. Tempoh terbaru ialah π

There is a phase shift of π/2 to the right.

PERHATIAN :Rujuk kepada bilai C =  π. Kemudian dibahagi dengan 2. Terdapat anjakan ke sebelah kanan sebanyak π/2. Kalau tanda (-), anjakan ke kanan. Kalau sebaliknya, ke kiri.  

There is a vertical shift of 1 up.

PERHATIAN :  Terdapat anjakan/tarikan  menaik sebanyak 1

So, let us handle these in pieces. We begin by graphing 3cos(2x), since it will look the same as cos(x), only with some changes to the labeling of the x- and y-axes.

 

* Lihat, nilai maksima = 3, nilai minima = -3, tempoh adalah π 

Figure 8 
Graph of y = 3cos(2x).

Now, we take into account the phase shift, which moves the graph to the right by π/2.

 

* Pindahkan ke kanan sebanyak π / 2 atau 90  

Figure 9:
Graph of y = 3cos(2x - π).

Lastly, we take into account the vertical shift, which moves the graph up 1, which gives us our final answer.

.

* Angkat lagi ke atas sebanyak 1. Nilai maksima terbaru = 4

Figure 10:  Graph of y=3cos(2x - π) + 1. 

Cuba anda fahami betul-betul graph yang saya  sediakan. Sekian dahulu untuk kali ini.

DISEDIAKAN PADA 4 OGOS 2012. 9.56 AM